Introducing to Graph

In this chapter we will talk about some definitions of graph, edge, arcs, loops, paths ...

Undirected Graph

Graph : A graph is a collection of edges and vertices.

Vertex : A vertex sometimes called node is a point where edges meet.

Edge : An edge has two nodes for its two end points.

Isolated node : Some node might not be the end point of any edge. These nodes are isolated.

Edge weighted graph : Numerical values are sometimes associated with edges specifying lengths or costs. They are sometimes called weighted graphs.

Weight : Weight is the value associated with the edge.

Self - loop : An edge is self - loop if it is of the form (u,u).

Simple graph : A graph is simple if it contains no self - loops and no repeated edges.

Multigraph : A graph is a multigraph if it contains self - loops or a edge more than once.

Incident edge : An edge (u,v) is incident to both vertex u and v.

Degree of vertex : The degree of a vertex is the number of edges which are incident to it.

Adjacent vertex :  Vertex u is adjacent to vertex v if there is a edge that connect them together.

Sparse : A graph is said to be sparse if the total number of edges is small compared to the number of possibilities (N*(N-1))/2.

Dense : If a graph is not sparse then it is dense.

Undirected graph : Undirected graph can go both way.

Directed graph

Directed graph : In a directed graph the edges have a direction. Directed graph are drawn with arrows to show direction.

Arcs : Arcs are edges in a directed graph. There is no edges in directed graph.

Out-degree of a vertex : the out-degree of a vertex is the number of arcs which begin at that vertex.

In-degree of a vertex : the in-degree of a vertex is the number of arcs which end at that vertex.

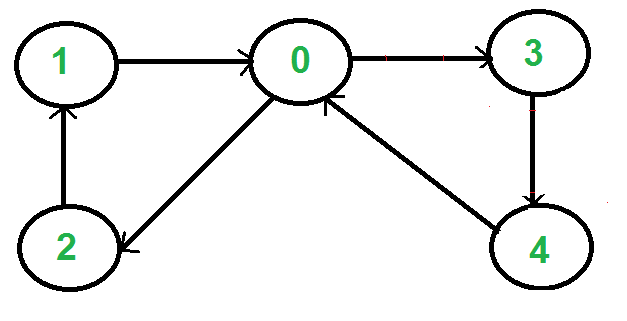
Paths

A path : A path from vertex u to vertex x is a sequence of vertices v0, v1 ... v_k such that v0 = u, vk = x and (v0, v1), (v1, v2), (v2, v3) ... are edges in the graph.

Reachable : Vertex x is said to be reachable from vertex u if a path exists from u to x.

Simple path : A path is simple if it contains no vertex more than once.

A cycle : A path is a cycle if it is a path from some vertex to itself.