The Big O notation is a commonly used notation to give a average time complexity. For exemple if I say walk 1km/hour for 10 hours then the time complexity is O(10) so O(N). N the number of hours. Usually in C++ you can do up to 10^7 operations. So if N=10^7, you must do O(N) or less. There is also two other notations a bit less popular : the Big Omega notation and the Big Theta notation. When you are working on a problem, it is important to analyse the time complexity and memory complexity. Oh yes, memory complexity ... You also use the Big O notation for memory complexity. It is also recommended to analyse memory complexity.
From Best Time Complexity to Worst Time Complexity, we have :
- O(1) constant
- O(log(n)) logarithm
- O(sqrt(n)) square root of n
- O(n) linear
- O(n*n)
- O(n^3) polynomial
- O(n!) or O(n^n) exponential
A few exercises :
for (int i=0; i<n; ++i){
// code
}
Time Complexity : O(n)
for (int i=0; i<n; ++i){
for (int j=0; j<n; ++j){
// code
}
}
Time Complexity : O(n^2)
for (int i=0; i<n; i += 2){
// code
}
Time Complexity : O(n) more precisely O(n/2)
int a=n;
while (a != 1){
a /= 2;
}
Time Complexity : O(log(n))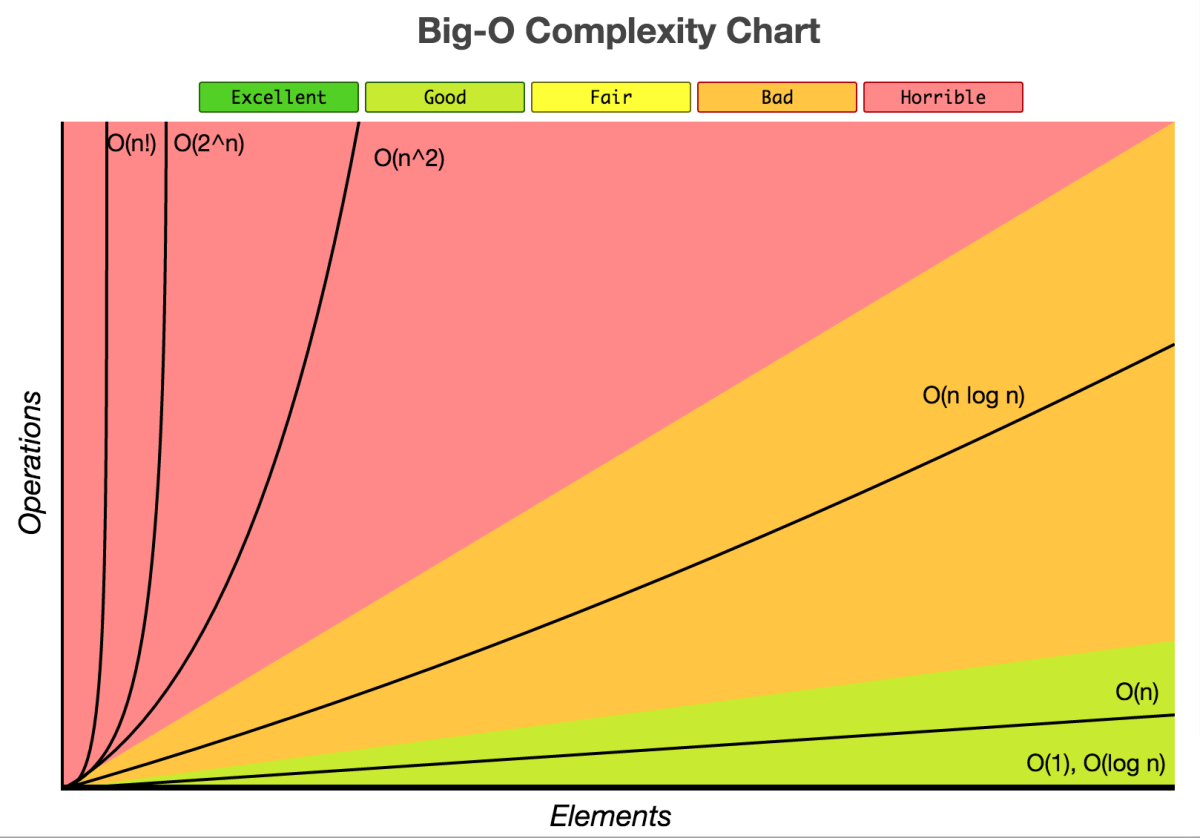

No comments:
Post a Comment