- https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=499
- https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=40
- https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=508
- https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=377
- https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=364
- https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=270
- https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=475
- https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=989
- https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=485
- https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1040
Thursday, 28 February 2019
Graph Exercises
To end our first course, I have prepared some graph exercises for you. All of them are UVA questions. I hope you enjoy them ! Next course will be about basic Math.
Wednesday, 27 February 2019
Topological Sort
Topological Sort is a classical algorithm applied on a Directed Acyclic Graph. In a DAG, you can always put the graph in a topological order. A topological is when you only have arrows pointing from a left node to a right node. Here is a exemple of a topolgical sort :

One possibility of topological ordering is 7 5 1 2 3 4 0 6. So here our goal is to find a technique that can help us to find a topological order. One technique is to do a vector<vector<int>> and to put all the node's fathers in it and then use recursion on all the empty nodes. Here is a C++ code that finds you a topological order. If this order doesn't exist then it will print -1 :

One possibility of topological ordering is 7 5 1 2 3 4 0 6. So here our goal is to find a technique that can help us to find a topological order. One technique is to do a vector<vector<int>> and to put all the node's fathers in it and then use recursion on all the empty nodes. Here is a C++ code that finds you a topological order. If this order doesn't exist then it will print -1 :
C++ code
#include <iostream>
#include <vector>
#include <unordered_set>
#include <algorithm>
using namespace std;
int N;
vector<unordered_set<int>> dad(1001);
vector<int> ret;
void topo(int node){
for (int i=1; i<=N; ++i){
if (!dad[i].empty()){
dad[i].erase(node);
if (dad[i].empty()){
ret.emplace_back(i);
topo(i);
}
}
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
int A;
cin >> N >> A;
for (int i=0; i<A; ++i){
int a,b;
cin >> a >> b;
dad[b].emplace(a);
}
vector<int> cand;
for (int i=1; i<=N; ++i){
if (dad[i].empty()){
ret.emplace_back(i);
cand.emplace_back(i);
}
}
for (auto& pos:cand) topo(pos);
if (ret.size() != N) cout << -1;
else{
for (auto& i:ret) cout << i << ' ';
}
return 0;
}
Tuesday, 26 February 2019
Floyed Warshal
Floyed Warshal is a classical graph algorithm. The Floyed Warshal algorithm assumes that the graph contains no negative cycles but if the graph has negative cycles the algorithm can still detect them. The Floyed Warshal algorithm is used to find all shortest paths. This algorithm works in O(n^3).
C++ code
#include <iostream>
#include <vector>
using namespace std;
const int INF=500*1000;
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n,a;
cin >> n >> a;
vector<vector<int>> adj(n+1,vector<int> (n+1));
// input reading
for (int i=0; i<a; ++i){
int inter1,inter2,dist;
cin >> inter1 >> inter2 >> dist;
adj[inter1][inter2] = dist;
adj[inter2][inter1] = dist;
}
// initialisation
vector<vector<int>> distance(n+1,vector<int> (n+1,INF));
for (int i=1; i<=n; ++i){
distance[i][i] = 0;
for (int j=1; j<=n; ++j){
if (adj[i][j]) distance[i][j] = adj[i][j];
}
}
// Floyed Warshal algorithm
for (int k=1; k<=n; ++k){
for (int i=1; i<=n; ++i){
for (int j=1; j<=n; ++j){
distance[i][j] = min(distance[i][j],distance[i][k]+distance[k][j]);
}
}
}
// printing
for (int i=1; i<=n; ++i){
bool first=true;
for (int j=1; j<=n; ++j){
if (!first) cout << ' ';
first = false;
cout << distance[i][j];
}
cout << '\n';
}
return 0;
}
I have found a alternative, it is a bit slower then Floyed - Warshal's algorithm (if you don't want to do Floyed Warshal). The idea of the alternative is to do a adjacent matrix and then perform n times Dijkstra's algorithm.
Monday, 25 February 2019
Google Kickstart Practice 2019
Google Kickstart is a competition organised by Google. The top competitors from Kick Start rounds may be invited to interview at Google ! Each Kick Start Round is open to all participants, no pre-qualification needed, so you can try your hand at one or give them all a shot.
The Practice round of Google Kickstart has already finished. By the way the algocorner team is ranked 411.
Practice round (idea) analysis :
The first question is a interactive question and the algorithm is just a simple binary search in log(n) per test case.
The second question can be done by a sliding window maximum algorithm or a partial sum.
The third question can be done by using Fermat's little theorem but the implementation of the idea is pretty hard.
Don't forget that there is also Round A the 24 March. Here is the link to the Kickstart Schedule : https://codingcompetitions.withgoogle.com/kickstart/schedule
This is one of Google's coding competition.
The Practice round of Google Kickstart has already finished. By the way the algocorner team is ranked 411.
Practice round (idea) analysis :
The first question is a interactive question and the algorithm is just a simple binary search in log(n) per test case.
The second question can be done by a sliding window maximum algorithm or a partial sum.
The third question can be done by using Fermat's little theorem but the implementation of the idea is pretty hard.
Don't forget that there is also Round A the 24 March. Here is the link to the Kickstart Schedule : https://codingcompetitions.withgoogle.com/kickstart/schedule
This is one of Google's coding competition.
Dijkstra's Algorithm
Dijkstra's Algorithm is a shortest path algorithm. The idea is just like BFS but instead of a queue we have a min priority_queue and now the graph is weighted. The only problem of Dijkstra's algorithm is that if it has a negative cycle then Dijkstra's algorithm will loop forever. This is why next time we will talk about Bellman-Ford algorithm, the Bellman-Ford algorithm can detect negative cycles and can just like Dijkstra's algorithm calculate the shortest path.
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> q;
C++ Code
The following line does min priority_queue :priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> q;
#include <iostream>
#include <vector>
#include <queue>
#include <climits>
#include <algorithm>
using namespace std;
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n,a,idx;
cin >> n >> a >> idx;
vector<int> ret(n,INT_MAX);
vector<vector<pair<int,int>>> adj(n);
for (int i=0; i<a; ++i){
int id1,id2,dist;
cin >> id1 >> id2 >> dist;
adj[id1-1].push_back({id2-1,dist});
adj[id2-1].push_back({id1-1,dist});
}
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> q;
q.emplace(idx-1,0);
ret[idx-1] = 0;
while (!q.empty()){
auto f=q.top();
q.pop();
for (auto& i:adj[f.first]){
if (ret[i.first] > i.second+f.second){
q.emplace(i.first,f.second+i.second);
ret[i.first] = f.second+i.second;
}
}
}
}
Sunday, 24 February 2019
Bellman - Ford
The Bellman - Ford algorithm is a classical graph algorithm. It can calculate the shortest path and is often used for negative cycle detection. The Bellman - Ford proceeds by relaxation just like the Dijkstra's algorithm. We can say that Bellman - Ford uses Dynamic Programming technique. Bellman - Ford runs in O(V*E).
C++ code
#include <bits/stdc++.h>
using namespace std;
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n,a;
cin >> n >> a;
vector<tuple<int,int,int>> adj;
for (int i=0; i<a; ++i){
int inter1,inter2,dist;
cin >> inter1 >> inter2 >> dist;
adj.emplace_back(make_tuple(inter1,inter2,dist));
}
vector ret(n+1,10000000);
ret[1] = 0;
for (int i=1; i<n; ++i){
for (auto& e:adj){
int a,b,w;
tie(a,b,w) = e;
ret[b] = min(ret[b],ret[a]+w);
}
}
int ab=ret[n];
for (auto& e:adj){
int a,b,w;
tie(a,b,w) = e;
ret[b] = min(ret[b],ret[a]+w);
}
if (ab == ret[n]) cout << ret[n];
else cout << "ERREUR";
return 0;
}
Saturday, 23 February 2019
Minimum Spanning Tree
In this article we will mainly be talking about Prim's algorithm and also a bit of Union Find.


Idea
There is two sorts of minimum spanning tree algorithm : Kruskal (Union-Find) and Prim (Greedy Algorithm). The two algorithm have the same complexity. Here is a two small illustrations so you could see the idea of the two algorithm.

Kruskal
Loads of people prefer Kruskal then Prim but I prefer Prim. Kruskal uses the Union Find algorithm. Union Find algorithm is a graph algorithm who uses a getcomp function to see if getcomp(a) == getcomp(b). If it does then a and b are in the same component. Else comp[getcomp(a)] = getcomp(b). Here is the function getcomp in C++:int getcomp(vector& comp,int a){
int compa=comp[a];
while (compa != comp[compa]){
compa = comp[compa];
}
comp[a] = compa;
return compa;
}
C++ Code - Prim
#include <iostream>
#include <vector>
#include <queue>
#include <set>
using namespace std;
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
int N,A,L,K1,K2,ret=0;
cin >> N >> A;
vector<vector<pair<int,int>>> adj(N+1);
for (int i=0; i<A; ++i){ cin >> K1 >> K2 >> L;
adj[K1].emplace_back(L,K2);
adj[K2].emplace_back(L,K1);
}
vector<int> vu(N+1);
vu[1]=1;
set<pair<int,int>> s;
for (auto& i:adj[1]) s.emplace(i);
while (!s.empty()){
auto f=*s.begin();
s.erase(s.begin());
if (vu[f.second]) continue;
ret += f.first;
vu[f.second]=1;
for (auto& i:adj[f.second]){
if (!vu[i.second]) s.emplace(i);
}
}
cout << ret;
return 0;
}
Friday, 22 February 2019
Breath First Scanning
Breath First Scanning is a flood fill algorithm who is commonly used and does not need any extra space. Here's the pseudo-code (no C++ code currently available) :
Every edge is traversed twice (once for each end-point), and each node is only marked once.
// component(i) denotes the // component that node i is in function flood_fill(new_component) do num_visited = 0 for all nodes i if component(i) = -2 num_visited = num_visited + 1 component(i) = new_component for all neighbors j of node i if component(j) = nil component(j) = -2 until num_visited = 0 function find_components num_components = 0 for all nodes i component(node i) = nil for all nodes i if component(node i) is nil num_components += 1 component(i) = -2 flood_fill(component,num_components)
Every edge is traversed twice (once for each end-point), and each node is only marked once.
Thursday, 21 February 2019
Flood Fill Algorithm
Flood fill can be performed in three basic ways : Depth First Search, Breath First Search and Breath First Scanning.
In the depth first formulation, the algorithm looks at each step through all of the neighbors of the current node and for those that have not been assigned to a component yet, assigns them to this component and recurces on them.
In breath first formulation, instead of recursing on new nodes, they are added to a queue.
In breath first scanning formulation, every node has two values : component and visited.
The depth first fomulation is the easiest to code and debug but it can require a large stack. The breath first fomulation is a bit better in memory as the queue is more efficient then the stack. The breath first scanning formulation is much better in memory however it is much slower : Time Complexity of N*N+M, where N is the number of vertices in the graph.
A Small Problem (taken from a book) to Warm Up :
In the depth first formulation, the algorithm looks at each step through all of the neighbors of the current node and for those that have not been assigned to a component yet, assigns them to this component and recurces on them.
In breath first formulation, instead of recursing on new nodes, they are added to a queue.
In breath first scanning formulation, every node has two values : component and visited.
The depth first fomulation is the easiest to code and debug but it can require a large stack. The breath first fomulation is a bit better in memory as the queue is more efficient then the stack. The breath first scanning formulation is much better in memory however it is much slower : Time Complexity of N*N+M, where N is the number of vertices in the graph.
A Small Problem (taken from a book) to Warm Up :
Street Race
Given a directed graph, and a start point and an end point. Find all points p that any path from the start point to the end must travel through p.
M <= 100 and N <= 50
Wednesday, 20 February 2019
Depth First Search
Idea
Depth First Search also called DFS is a classical algorithm just like BFS. It does recursive calls to find the solution. This algorithm is easier to implement then the BFS, this is why it is very popular in the competitive programming community. It has the same complexity then the BFS. One of the only problems of the DFS is that he uses loads of memory because it uses a recursive stack. The recursive stack is a stack where there is all your recursive calls. Each time it pops the last element of the stack.Pseudo-code
Here we are implementing the DFS with adj as adjacent list, beg as the begin node, end as the end node, vu is a table of boolean. We are trying to implement a algorithm who tells you if you can go from beg to end.DFS(adj,beg,end,vu) {
if beg == end return true
for all neighbors in adj {
if !vu[neighbors] {
vu[neighbors]=true;
DFS(adj,neighbor,end,vu)
vu[neighbors]=false;
}
}
return false
}
C++ Code
#include <iostream>
#include <vector>
using namespace std;
inline bool DFS(vector<vector>& adj,vector& vu,int beg,int end){
if (beg == end) return true;
for (auto& neighbour:adj[beg]){
if (!vu[neighbor]){
vu[neighbour]=true;
DFS(adj,vu,neighbour,end);
vu[neighbour]=false;
}
}
return false;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
int n,m;
// initiation
// n the number of vertices, m the number of edges
cin >> n >> m;
vector<vector> adj(n);
for (int i=0; i<m; ++i){
int a,b; // directed graph a to b
cin >> a >> b;
adj[a].emplace_back(b);
}
vector vu(n);
if (DFS(adj,vu,0,n-1)) cout << "POSSIBLE\n";
else cout << "IMPOSSIBLE\n";
return 0;
}
Applications
DFS and BFS have a lot of same applications but some are unique to BFS and some are unique to DFS.- Finding Strongly Connected Components of a graph
- To test if a graph is bipartite
- Topological Sorting
- Path Finding
- Detecting cycle in a graph
- Minimum Spanning Tree
- All pair Shortest path
- ......
Tuesday, 19 February 2019
Breath First Search
Idea
Breath First Search expands the shallowest node in the tree first. BFS mostly uses a adjacent list. It is complete, optimal for unit-cost operators and has time and space complexity of O(V+E). If you don't know the big O notation please read the big O notation article first.Pseudo - code
Here we are calculating the shortest path between beg and end, we suppose there are less then one million edges and it is not a weighted graph :BFS (adj,beg,end){
initialize Q = {{beg,0}} // a queue with {node,sum}
initialize a vu table with 1000000 as initial value
while (Q not empty){
f = top element of Q
dequeue(Q)
for all neighbors in adj {
if vu[neighbors] > f.sum {
vu[neighbors] = f.sum
add {neighbors,f.sum+1} to Q
}
}
}
return vu[end]
}
C++ code
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
struct vertex{
int node,sum;
};
int n,m;
inline int BFS(vector<vector>& adj,int beg,int end){
queue q;
q.emplace(beg,0);
vector vu(n,1000000);
while (!q.empty()){
auto f = q.front();
q.pop();
for (int& neighbor:adj[f.node]){
if (vu[neighbor] > f.sum+1){
vu[neighbor] = f.sum+1;
q.emplace(neighbor,f.sum+1);
}
}
}
return vu[end];
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
// initiation
// n the number of vertices, m the number of edges
cin >> n >> m;
vector<vector> adj(n);
for (int i=0; i<m; ++i){
int a,b; // directed graph a to b
cin >> a >> b;
adj[a].emplace_back(b);
}
BFS(adj,0,n-1);
return 0;
}
Applications
Here is a small list of the applications of BFS. BFS can be used for :- Shortest path and minimum spanning tree
- GPS Navigation systems
- Ford - Fulkerson algorith,
- To test if a graph is bipartite
- Path Finding
- ......
Monday, 18 February 2019
Big O notation
The Big O notation is a commonly used notation to give a average time complexity. For exemple if I say walk 1km/hour for 10 hours then the time complexity is O(10) so O(N). N the number of hours. Usually in C++ you can do up to 10^7 operations. So if N=10^7, you must do O(N) or less. There is also two other notations a bit less popular : the Big Omega notation and the Big Theta notation. When you are working on a problem, it is important to analyse the time complexity and memory complexity. Oh yes, memory complexity ... You also use the Big O notation for memory complexity. It is also recommended to analyse memory complexity.
From Best Time Complexity to Worst Time Complexity, we have :
From Best Time Complexity to Worst Time Complexity, we have :
- O(1) constant
- O(log(n)) logarithm
- O(sqrt(n)) square root of n
- O(n) linear
- O(n*n)
- O(n^3) polynomial
- O(n!) or O(n^n) exponential
for (int i=0; i<n; ++i){
// code
}
Time Complexity : O(n)
for (int i=0; i<n; ++i){
for (int j=0; j<n; ++j){
// code
}
}
Time Complexity : O(n^2)
for (int i=0; i<n; i += 2){
// code
}
Time Complexity : O(n) more precisely O(n/2)
int a=n;
while (a != 1){
a /= 2;
}
Time Complexity : O(log(n))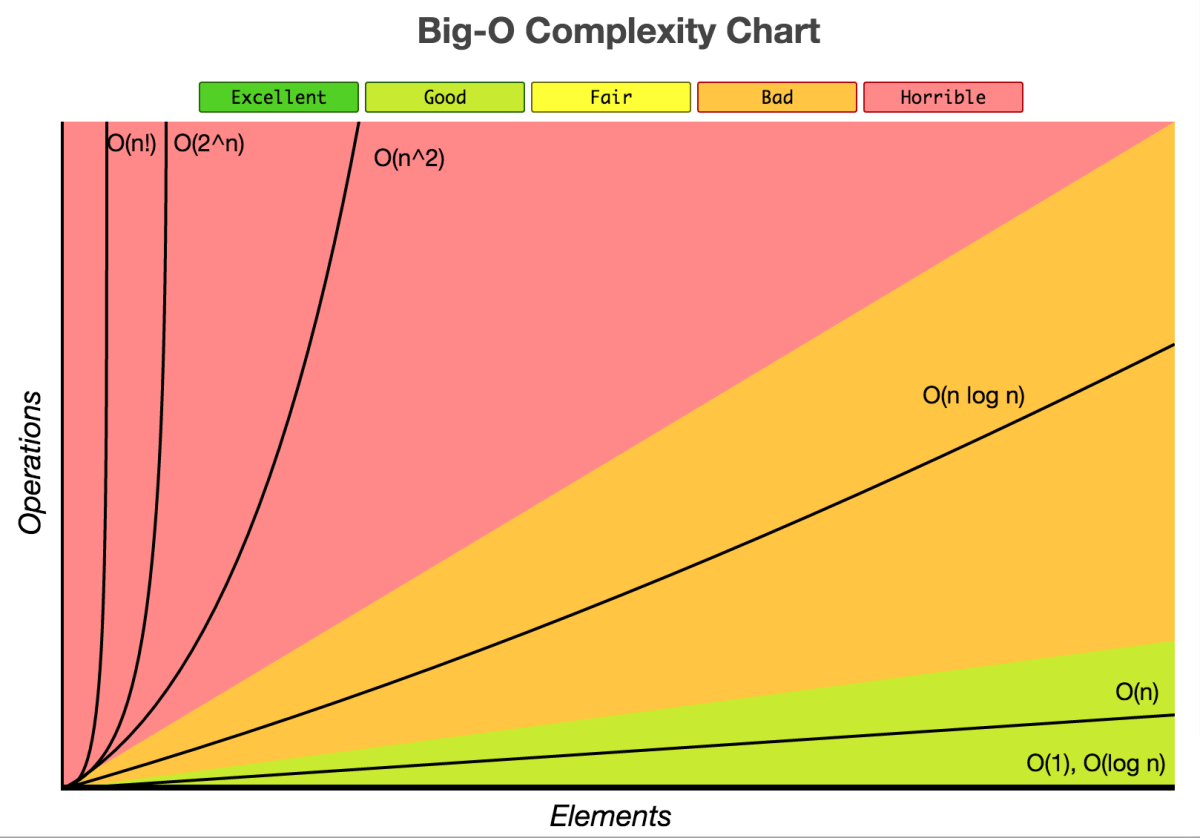
Tips and C++ template
C++ template
My C++ template :#include <iostream>
using namespace std;
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << 4 << '\n';
return 0;
}
- Line 1 : the basic include of C++
- Line 2 : to remove all std:: for exemple you don't need to write std::cin >> a; anymore you just need to write cin >> a;
- Line 4 : the main function, inside of it you put your code.
- Line 5 : optimisation. You could also use ios::base_with_stdio(0);
- Line 6 : optimisation for reading input
- Line 7 : optimisation for printing output
- Line 8 : prints 4 with a new line. '\n' is faster than endl
- Line 9 : for safety we return 0 at the end
#include <bits/stdc++.h>
#pragma GCC optimize("Ofast")
#pragma GCC optimize("O3")
#include <ext/pb_ds/assoc_container.hpp> using namespace __gnu_pbds; using indexed_set = tree<int, null_type, less<inr>, rb_tree_tag, tree_order_statistics_node_update>;
// using indexed set
indexed_set s;
s.insert(2);
// insert 2
auto x = s.find_by_order(0);
// returns iterator of the element position 2
cout << *x << '\n';
// prints 2
cout << s.order_of_key(2) << '\n'; // 0
// prints the position of 2
- The first part includes everything. All the includes. We recommand it but for exemple on a MacBook you need to install some stuff to use this.
- This can do optimisation if g++ didn't optimise for you.
- This can also do optimisation if g++ didn't optimise for you.
- This is the tings to include if you want to use a indexed_set
- This is operations you can use for a indexed_set .order_of_key(2) and .find_by_order(0); are O(log(n)). The next post will be talking about the big O notation if you don't already know what this means.
Informed and Uninformed Search
Uninformed Search
Searching is a process of considering possible sequences of actions.A problem consists of four parts : the initial state, a set of operators, a goal test function and a path cost function. Search algorithms are judged on the basis of completeness, optimality, time complexity, space complexity. Uninformed search is also sometimes called blind search.
Exemples of uninformed search : Breath First Search, Depth First Search, DF-ID, IDS ...
Informed Search
Unlike Uninformed Search, Informed Search knows some informqtion that can help us to improve path selection with generally a distance function (ex. Mahattan distance, Euclidean distance) or some direction (ex. If we prefer south then the search will be towards south direction).Exemples of informed search : Best First Search, Heuristic Search such as A*.
Different Graph
Subgraphs : The subgraph G induced by V' is the graph (V',E').
Induced : The subgraph G' has everything taken from G.
A chain : it's a special graph where two nodes have a degree of one and all the other ones have a degree of two
A star : one node has n-1 neighbours and the other ones have a degree of one.
Tree : An undirected graph is said to be a tree if it contains no-cycle (acyclic) and is connected.
Binary tree : A binary tree is a tree where each node has a parent (except the root) and up to two children. A perfect binary tree is a binary tree in which all interior nodes have two children and all leaves have the same depth or same level.
A binary tree : it's a special tree where each parent has one or two children.
A multigraph : it's a graph that can have multiple edges between two same points.
A self loop : it's when a node loops on itself.
A bipartite graph : it's a graph who can be coloured with two colours such that two nodes of the same colour don't have any edges in commun.
A weighted graph : it's a graph such that each edge has a weight.
A directed graph : it's when the edges have a direction.
A rooted tree : A rooted tree is a tree where there is a notion of the "top" node, which is called the root. Thus, each node has one parent and has any number of children.
Forest : A forest is an undirected graph which contains no cycle.
DAG: Directed Acyclic Graph
Complete graph : A graph is said to be complete if there is an edge between every pair of vertices
Bipartite graph : A graph is said to be bipartite if the vertices can be split into two sets V1 and V2 such there are no edges between two nodes of V1 or two nodes of V2.
Acyclic : no cycle
Induced : The subgraph G' has everything taken from G.
A chain : it's a special graph where two nodes have a degree of one and all the other ones have a degree of two
A star : one node has n-1 neighbours and the other ones have a degree of one.
Tree : An undirected graph is said to be a tree if it contains no-cycle (acyclic) and is connected.
Binary tree : A binary tree is a tree where each node has a parent (except the root) and up to two children. A perfect binary tree is a binary tree in which all interior nodes have two children and all leaves have the same depth or same level.
A binary tree : it's a special tree where each parent has one or two children.
A multigraph : it's a graph that can have multiple edges between two same points.
A self loop : it's when a node loops on itself.
A bipartite graph : it's a graph who can be coloured with two colours such that two nodes of the same colour don't have any edges in commun.
A weighted graph : it's a graph such that each edge has a weight.
A directed graph : it's when the edges have a direction.
A rooted tree : A rooted tree is a tree where there is a notion of the "top" node, which is called the root. Thus, each node has one parent and has any number of children.
Forest : A forest is an undirected graph which contains no cycle.
DAG: Directed Acyclic Graph
Complete graph : A graph is said to be complete if there is an edge between every pair of vertices
Bipartite graph : A graph is said to be bipartite if the vertices can be split into two sets V1 and V2 such there are no edges between two nodes of V1 or two nodes of V2.
Acyclic : no cycle
Graph Properties
A graph can be connected, strongly connected and a graph can have different properties ...
Connected undirected graph : An undirected graph is said to be connected connected if there is a path from every vertex to every other vertex.
A component : A component of a graph is a maximal subset of the vertices such that every vertex is reachable from each other vertex in the component.
Strongly connected directed graph : A directed graph is said to be strongly connected if there is a path from every vertex to every other vertex.
A strongly connected component of a directed graph : is a vertex u and the collection of all vertices v such that there is a path from u to v and a path from v to u.
Connected undirected graph : An undirected graph is said to be connected connected if there is a path from every vertex to every other vertex.
A component : A component of a graph is a maximal subset of the vertices such that every vertex is reachable from each other vertex in the component.
Strongly connected directed graph : A directed graph is said to be strongly connected if there is a path from every vertex to every other vertex.
A strongly connected component of a directed graph : is a vertex u and the collection of all vertices v such that there is a path from u to v and a path from v to u.
Graph Course 1
This course will cover most (easy) graph subjects in 17 days. It will also have a article about the Big O notation and a article about C++ template. We will publish one article per day until this course is finish.
Started : Tuesday 12 February 2019
Ending : Sunday 28st March 2019
Here is the courses content :
Started : Tuesday 12 February 2019
Ending : Sunday 28st March 2019
Here is the courses content :
- Introducing to Graph
- Graph Representations
- Graph Properties
- Different Graph
- Informed and Uninformed Graph
- Tips and C++ template
- Big O notation
- Breath First Search
- Depth First Search
- Flood Fill Algorithms
- Breath First Scanning
- Minimum Spanning Tree
- Dijkstra's Algorithm
- Bellman - Ford
- Floyed Warshal
- Topological Sort
- Graph Exercises
Graph Representation
There are in total a few different graph representation + implicit representation :
Implicit Representation : For some graphs,the graph itself does not have to be stored.
Edge List : List of pairs of vertices.
Ex : (1,3),(2,3),(3,3),(5,3),(4,5),(2,4),(1,2)
Adjacency Matrix : This is a N* (N array). N is the number of vertices. If node i is connected to node j then adj[i][j] = 1 else adj[i][j]=0. Ex :
Sometimes a grid can also be a good representation.
Adjacent List : Keep track all the edges incident to a given vertex and do this for all vertex. Ex :
Implicit Representation : For some graphs,the graph itself does not have to be stored.
Edge List : List of pairs of vertices.
Ex : (1,3),(2,3),(3,3),(5,3),(4,5),(2,4),(1,2)
Adjacency Matrix : This is a N* (N array). N is the number of vertices. If node i is connected to node j then adj[i][j] = 1 else adj[i][j]=0. Ex :
Sometimes a grid can also be a good representation.
Adjacent List : Keep track all the edges incident to a given vertex and do this for all vertex. Ex :
1 : 3,2 2 : 3,4 3 : 3 4 : 5 5 : 3
A graph making website: https://csacademy.com/app/graph_editor/
Introducing to Graph
In this chapter we will talk about some definitions of graph, edge, arcs, loops, paths ...
Vertex : A vertex sometimes called node is a point where edges meet.
Edge : An edge has two nodes for its two end points.
Isolated node : Some node might not be the end point of any edge. These nodes are isolated.
Edge weighted graph : Numerical values are sometimes associated with edges specifying lengths or costs. They are sometimes called weighted graphs.
Weight : Weight is the value associated with the edge.
Self - loop : An edge is self - loop if it is of the form (u,u).
Simple graph : A graph is simple if it contains no self - loops and no repeated edges.
Multigraph : A graph is a multigraph if it contains self - loops or a edge more than once.
Incident edge : An edge (u,v) is incident to both vertex u and v.
Degree of vertex : The degree of a vertex is the number of edges which are incident to it.
Adjacent vertex : Vertex u is adjacent to vertex v if there is a edge that connect them together.
Sparse : A graph is said to be sparse if the total number of edges is small compared to the number of possibilities (N*(N-1))/2.
Dense : If a graph is not sparse then it is dense.
Undirected graph : Undirected graph can go both way.

Arcs : Arcs are edges in a directed graph. There is no edges in directed graph.
Out-degree of a vertex : the out-degree of a vertex is the number of arcs which begin at that vertex.
In-degree of a vertex : the in-degree of a vertex is the number of arcs which end at that vertex.
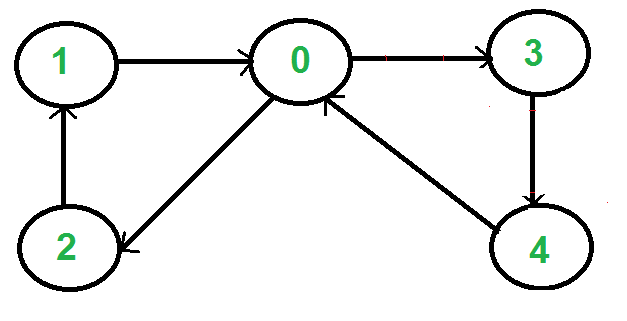
Reachable : Vertex x is said to be reachable from vertex u if a path exists from u to x.
Simple path : A path is simple if it contains no vertex more than once.
A cycle : A path is a cycle if it is a path from some vertex to itself.
Undirected Graph
Graph : A graph is a collection of edges and vertices.Vertex : A vertex sometimes called node is a point where edges meet.
Edge : An edge has two nodes for its two end points.
Isolated node : Some node might not be the end point of any edge. These nodes are isolated.
Edge weighted graph : Numerical values are sometimes associated with edges specifying lengths or costs. They are sometimes called weighted graphs.
Weight : Weight is the value associated with the edge.
Self - loop : An edge is self - loop if it is of the form (u,u).
Simple graph : A graph is simple if it contains no self - loops and no repeated edges.
Multigraph : A graph is a multigraph if it contains self - loops or a edge more than once.
Incident edge : An edge (u,v) is incident to both vertex u and v.
Degree of vertex : The degree of a vertex is the number of edges which are incident to it.
Adjacent vertex : Vertex u is adjacent to vertex v if there is a edge that connect them together.
Sparse : A graph is said to be sparse if the total number of edges is small compared to the number of possibilities (N*(N-1))/2.
Dense : If a graph is not sparse then it is dense.
Undirected graph : Undirected graph can go both way.
Directed graph
Directed graph : In a directed graph the edges have a direction. Directed graph are drawn with arrows to show direction.Arcs : Arcs are edges in a directed graph. There is no edges in directed graph.
Out-degree of a vertex : the out-degree of a vertex is the number of arcs which begin at that vertex.
In-degree of a vertex : the in-degree of a vertex is the number of arcs which end at that vertex.

Paths
A path : A path from vertex u to vertex x is a sequence of vertices v0, v1 ... v_k such that v0 = u, vk = x and (v0, v1), (v1, v2), (v2, v3) ... are edges in the graph.Reachable : Vertex x is said to be reachable from vertex u if a path exists from u to x.
Simple path : A path is simple if it contains no vertex more than once.
A cycle : A path is a cycle if it is a path from some vertex to itself.
Welcome on Algocorner !
This site will contain all the algorithms and notions that you will need for an interview or a competition. We will provide for each algorithm a C++11 code and a idea or a pseudo-code. We will also provide some articles on the syntax of C++ for beginners.
Algorithm : It's a sequence of operation. This sequence transforms an input into an output.
C++ : It's a programming language whose library contains all sorts of containers (ex. set, map). This library is often called the STL (Standard Template Library). This programming language is one of the fastest. Here, we use C++11, it's the C++ 2011 version.
Algorithm : It's a sequence of operation. This sequence transforms an input into an output.
C++ : It's a programming language whose library contains all sorts of containers (ex. set, map). This library is often called the STL (Standard Template Library). This programming language is one of the fastest. Here, we use C++11, it's the C++ 2011 version.
Subscribe to:
Comments (Atom)
std::next_permutation(arr.begin(),arr.end());
What is next_permutation(a.begin(),a.end()) ? Next permutation is like what its name says, finds the next permutation of a and assigns ...
-
I really enjoyed this contest ! The questions were nice and I had a lot of time to do them. So here I want to share my approaches to the pro...
-
Usage of __int128_t: supports really big intermediate numbers, from -2^128 + 1 to 2^128 - 1 it has 128 bits Usage of __float128 : ...
-
Time : 30 minutes Question Optimise this function : f(int n){ if (n == 0) return 1; if (n == 1) return 2; return f(n-1)+...
